Фоменко Анатолий
Фоменко Анатолий Тимофеевич (1945) — доктор математических наук, профессор, академик РАН, художник -график. Автор «Новой хронологии».
Родом из Донецка.
Алгеброй поверить гармонию… Кто в запале не выпускал, как птицу из рукава, зто крылатое выражение?
А здесь всё наоборот: не искусство под обнажающим контролем алгебры, а математика, поверяемая оплодотворяющей силой живописи. Неужто бывает такое?
И придумал этот невероятный переворот не кто-либо из художников-модернистов, а член-корреспондент Академии наук, профессор кафедры высшей геометрии и топологии Московского университета Анатолий Тимофеевич Фоменко. Молодой специалист в области компьютерной геометрии, вариационного исчисления, он создал новую теорию топологии. Он автор 140 научных трудов, многие из них изданы за рубежом на английском, французском, японском языках. Лауреат нескольких научных премий. Казалось бы устойчивая профессия — этакий типичный «синий чулок» в академическом смокинге.
А тут — художник… Да еще какой!
Из цикла «Мастер и Маргарита», роман М.Булгакова. Кот Бегемот наблюдает за казнью Иешуа.
Ведь он в стремлении мыслить образами замахнулся на невероятное -пытается вложить математические положения в ассоциативные образы искусства. И это ему удается, видимо, потому, что талантливый человек, как говорят, талантлив во всем — и у компьютера, и у мольберта. Картины Фоменко не вещают, вопиют об этом.
Портрет жены.
Как рождаются эти «немыслимые» мысленные образы в душе прославленного математика и талантливого живописца, не нам судить. Все это уже глубинный мир не только математики — это чудо переплетения точной науки с философией, историей, эстетикой и торжество этого заветного и неповторимого, чем обладает многосторонняя душа самого творца.
Итак, откровение ученого…
У каждого профессионального математика имеется свой комплекс представлений о внутренней геометрии известного ему математического мира и наглядных образах, с которыми ассоциируются те или иные абстрактные математические понятия в алгебре, теории чисел, математическом анализе и т. д. Чрезвычайно интересно тем не менее, что, как показывает опыт, у разных математиков одни и те же абстракции часто рождают примерно одинаковые наглядные представления. В большинстве случаев их довольно трудно изобразить. Однако важно, что они реально существуют, проявляясь в устном общении математиков, помогая им лучше понять друг друга.
Теория вероятностей. Процесс образования нормального или «гаусова» распределения.
Графический материал — это попытка как бы сфотографировать изнутри сложный, своеобразный мир, богато населенный образами и понятиями, составляющими предмет современной математики. Все сюжеты либо основаны на совершенно конкретных математических конструкциях, идеях, теоремах, изображают реальные математические объекты и процессы, либо отражают различные приемы восприятия тех или иных абстрактных математических понятий, например, бесконечности, непрерывности, гомеоморфизма, гомотопии и т. д.
Из цикла «Беседы с авторами 16-го века». Искушение Святого Антония. Иллюстрация общего понятия математической бесконечности.
Геометрическое воображение и интуиция играют огромную роль в современных математических исследованиях, в особенности связанных с математической физикой, геометрией, топологией. Во многих глубоких научных математических работах, посвященных сложным специальным вопросам, активно используется «наглядный жаргон», выработанный при исследовании двухмерных и трехмерных образов. Вроде — «разрежем поверхность», «склеим листы поверхности», «приклеим цилиндр», «вывернем сферу наизнанку», «присоединим ручку». Такая терминология — не прихоть математиков, а «производственная необходимость», поскольку ее употребление и само математическое мышление в терминах этих образов совершенно необходимы при доказательстве многих технически невероятно трудных результатов. Часто доказательство того или иного математического факта удается сначала «увидеть» в геометрических терминах, а лишь затем оформить в виде логически непротиворечивого рассуждения. Иногда это очень трудно и требует серьезных затрат интеллектуальной энергии. Однако целесообразность таких затрат психологически оправдывается наглядной и красивой геометрической картиной, уже сложившейся в голове исследователя и убеждающей его в правильности избранного пути. Таким образом, критерий красоты геометрического образа служит компасом для выбора оптимального пути дальнейшего формально-логического доказательства.
Из цикла «Беседы с авторами 16-го века». «Антибрейгель», вариации на тему «Алхимики». Математическое понятие бесконечности; общая идея непрерывной деформации объектов.
Автор многие годы читает курс «Дифференциальной геометрии и топологии» в МГУ и по собственному опыту знает, насколько полезно иногда проиллюстрировать то или иное сложное математическое понятие рисунком. Это помогает студентам быстрее вникнуть в задачу. В этом смысле многие мои работы имеют именно такой, утилитарный характер. Не следует, конечно, думать, что они идеально соответствуют своим математическим «прототипам». Сюжет каждой работы построен на сугубо субъективных ассоциациях и передает лишь авторское восприятие того или иного математического «персонажа». Это не чертеж, в нем не соблюдены размеры и пропорции; более того, часто математический объект задает лишь тему, эмоционально-фантастической вариацией на которую и является графическая композиция. Однако тема — математический образ или конструкция — является в большинстве работ их главным центром, информационным фокусом. Она, как правило, вполне узнаваема специалистами, знакомыми с данным математическим объектом (в виде формул, определений, теорем). Тема обрастает вариациями, как в музыке (и аналогия здесь не случайна), причем эти вариации отнюдь не являются только фоном или украшением. В них проявляется эмоциональный настрой автора, его видение основной темы, отношение к ней, иногда — ряд сложных ассоциаций, сплетающих центральный образ с другими, совсем далекими, но в чем-то неожиданно близкими, в единое целое.
Из цикла «Беседы с авторами 16-го века. «Антидюрер», вариации на тему знаменитой гравюры Дюрера «Меланхолия».
При этом немало объективных трудностей, возникающих на этом пути. Невозможно, например (да и не нужно), идеально точно нарисовать объект, «живущий», скажем, в семимерном пространстве. Мы привыкли воспринимать лишь трехмерные образы, следовательно, такой персонаж поневоле искажается, будучи принудительно помещен в трехмерное пространство. Приходится иногда жертвовать точностью в пользу наглядности. Тем не менее во многих случаях этот наглядный образ сохраняет важнейшие черты своего оригинала.
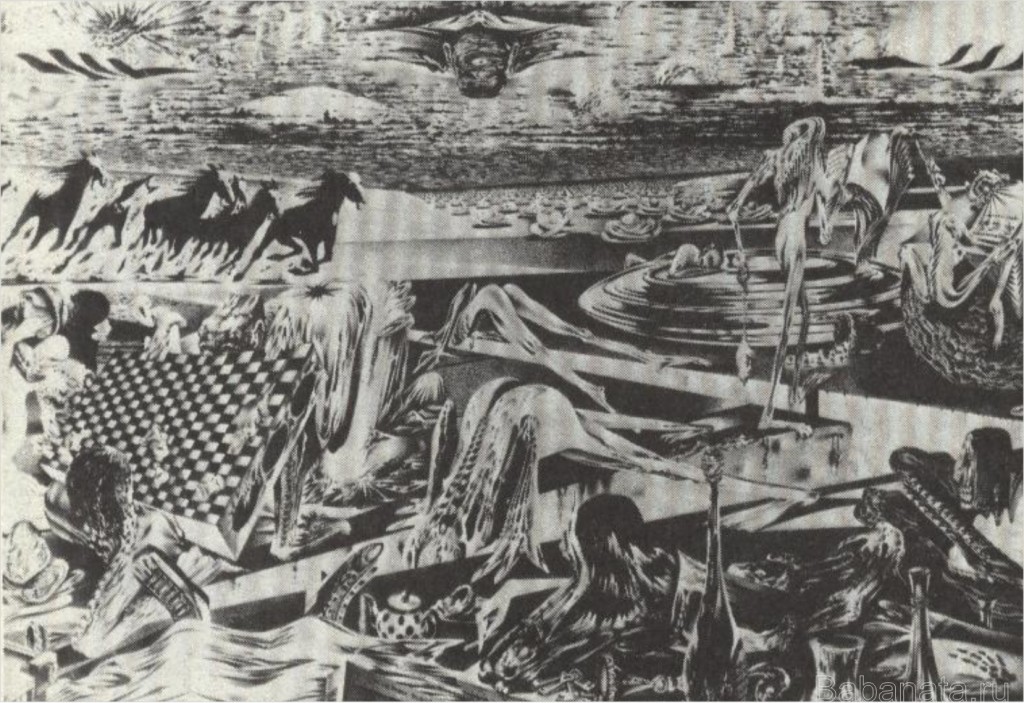
Из цикла «Мифы». Скандинавия. Гибель Валгаллы. Топологическая перестройка поверхностей уровня гладкой функци.
Многие работы автор старался выполнить в шутливом тоне. Дело в том, что «серьезное», стандартное изображение, например, двухмерной сферы с пятью ручками стало настолько привычным в учебниках по геометрии, что не позволяет обратить внимание на некоторые глубокие, но неочевидные свойства этого объекта. Такова судьба любых
многократно тиражируемых канонических изображений: их образ становится привычным и не останавливает взгляд зрителя. Внесение некоторой эмоциональности в изображение открывает, на мой взгляд, большие возможности. Здесь, как и в жанре карикатуры, можно ярко акцентировать то или иное свойство, деталь и т. п. Поэтому автор не сдерживал себя в тех случаях, когда предоставлялась возможность придать рисунку юмористический колорит и выразительность. Именно в этом причина моего стремления апеллировать скорее к эмоциям зрителя, чем к рациональной части его мышления. Впрочем, насколько это удалось — судить читателям.
Рождение бога грома Тора. Начало геометрического процесса построения «сферы Александера».
Почти все мои картины, кроме математики, содержат «второй слой» информации. Речь идет о внематематических ассоциациях, неизбежно возникавших у автора в процессе работы. Ассоциации причудливы и эмоционально разнообразны. То это шутка и желание увидеть в той же сфере с пятью ручками забавное необычное существо, то гротеск, неожиданно смешивающий, искажающий все привычные пропорции и масштабы, заставляющий подивиться совсем обычным вещам. То ирония, грусть или даже страдание, которые так же изначально заключены в сочетаниях неживых геометрических линий и фигур, как и в живых, и надо лишь подчеркнуть их.
Из цикла мифы. Скандинавия. Легенда о Брунгильде погружённой в сон богом Вотаном на скале, окружённой огнём. Фрактальные множества. Предельные точки сложных систем дифференциальных уравнений.
Отражая мировоззрение автора, работы имеют неизбежный философский аспект, в основе которого лежат реально существующие, иногда непривычные, неожиданные связи и аналогии. Единство и взаимопроникновение эмоции и формы, формы и движения, развития и времени, живого и неживого, материальных вещей и абстрактных понятий (т. е. мира вещей и мира тонких энергий, говоря языком восточных философов) — вот что стремился отразить автор во многих своих композициях.
Из цикла «Мифы». Древняя Индия. Легенда об огненном драконе.
В каждой из них — попытка сказать многое, и словами краткого комментария или в названии работы выразить все невозможно. Большинство зрителей — не математики. При всем желании им трудно вникнуть в математический смысл картины. Поэтому первоначально автор знакомил со своими работами только математическую аудиторию, внутри которой язык математических символов и понятий общепринят. Однако выяснилось, что часто они вызывают большой интерес у зрителей, не имеющих никакого отношения к современной математике (что, безусловно, радует и стимулирует автора). Эта категория зрителей неожиданно увидела во многих работах образы, отсутствовавшие в первоначальном авторском замысле, но (что удивительно) прекрасно соответствовавшие их духу и композиции. Мне всегда хотелось пробудить фантазию зрителя, вызвать у него какие-то собственные ассоциации и толкования. Мысль о таком раскрепощении зрительского сознания постоянно присутствовала при создании работ. Большинство внематематических ассоциаций связано с мифологией разных народов, древними обычаями, культами, средневековыми литературными произведениями. В этом проявляются литературные, исторические и другие интересы и увлечения автора. , Возможно, другие читатели увидят в этих работах нечто совсем иное.
Несколько слов о технике работы. Обычно, когда у меня появлялось настроение и идея новой композиции, она создавалась «сразу», т. е. без перерывов даже на день. Проб и эскизов я, как правило, не делаю. Каждая работа -в определенной степени экспромт. Конечно, всегда имеется некий общий план, однако настолько смутный, что он
не поднимается выше подсознательного уровня. В процессе заполнения листа композицией каждый ее фрагмент сразу отделывается до окончательного вида. Поэтому постоянно присутствует угроза, что композиция, разрастающаяся на листе, «не замкнется». Такое иногда случалось, и работа безжалостно выбрасывалась.
Хотелось бы еще отметить, что благодаря отсутствию специального художественного образования автор никогда не ограничивал себя рамками какого-либо жанра графики или живописи. Возможно, определенное влияние оказали стили моих любимых художников Босха, Брейгеля, Дали, Эшера, Бёклина, хотя сознательного подражания им никогда не было.
Анатолий Фоменко.
Журнал Ч. и П..
На Дни «Комсомольской правды», которые газета проводила в Красноярском крае. «Клуб любознательных» взял с собой выставку работ доктора физико-математических наук, профессора МГУ Анатолия Тимофеевича Фоменко — нашего старого друга и героя.
Па четвертом курсе университета, когда в пору было думать о дипломе, студент Фоменко вдруг решил перевестись с отделения механики на отделение математики — шаг, согласитесь. достаточно рискованный. А для этого пришлось досдавать множество предметов, о которых раньше он имел весьма смутное представление, среди них — топологию. Готовясь к экзамену, Анатолий начал рисовать формулы, придумывать на их мотивы некие сюжеты. Сложнейший материал запоминался так действительно намного легче…
В результате уже через год после того, как впервые взял pyки учебник топологии. Фоменко выпустил учебник собственный — с картинками.
В Красноярске на выставку Фоменко ходили очень требовательные и квалифицированные зрители: она была развернута в Доме ученых академгородка. И тетрадь отзывов с подписями членкоров, докторов и кандидатов наук сохраняет слова восхищения — и художником, и математиком.
«2-адический соленоид»…
Попробуйте провести крошечное социологическое исследование. Выберите наугад, скажем, тридцать человек и попросите их ответить на вопрос: «Трудна ли, по вашему мнению, математика?» — а тех, кто ответит утвердительно, спросите: «Если, как вы считаете, математика трудна для восприятия, то чем это объяснить?» Ответы на второй вопрос, как это часто делают социологи, можно предусмотреть заранее, например: «Математика слишком абстрактна, она не имеет связи с реальной жизнью», «В одних формулах и обозначениях черт ногу сломит» или «Все это выдумки людей, которые не способны на настоящее дело». Ответы можно обработать, выявив частоту того или иного высказывания в определенной группе опрашиваемых, и, как это обычно бывает при социологических опросах, вы получите больше информации об аудитории, чем о самом предмете опроса — в данном случае математике.
Этот микроэксперимент скорее всего покажет, что в современной культуре математические идеи наталкиваются на некоторое сопротивление. Представители многих «интеллектуальных» профессий, таких, как философия, история, юриспруденция, психология и даже экономика и биология, за очень редким исключением ведут свои дискуссии без какого бы то ни было привлечения математических аргументов. Трудно понять, какие именно общественные механизмы привели к «вымыванию» математики из культурного арсенала образованного человека, может быть, «обязаловка» перегруженных школьных программ или отсутствие наглядных и красивых изображений, захватывающе реализуемых сегодня средствами компьютерной графики. Ясно одно: рефлекс избегания математики сильно ограничивает познавательные возможности человека.
Математическая фантазия на темы средневековых мифов и легенд. Зарождение современных математических абстрактных понятий ¦ науке средних веков. Ученые того времени часто оперировали понятиями, которые хотя и не оправдали себя в дальнейшем, тем не менее помогли открыть многие важнейшие законы механики, математики и физики. Весьма часто ошибочные форма и терминология скрывали правильные законы, интуитивно нащупанные пытливым интеллектом.
Если обратиться к истории, то можно сделать вывод, что раньше культурное сопротивление математическим идеям было гораздо меньше. В эпоху Возрождения европейская культура охотно восприняла алгебру, пришедшую с Ближнего Востока,
и геометрию, исчерпывающим образом разработанную древними греками. Именно в Греции в IV веке до нашей эры впервые появился профессиональный ученый — человек, посвящающий свою жизнь развитию науки (такой наукой была как раз математика) и получающий за это вознаграждение. Эллинское общество ценило своих математиков, и, может быть, это послужило причиной того, что, кроме Библии, в истории цивилизации существует только одна книга, изучавшаяся и переиздававшаяся чаще других на протяжении тысячелетий,— «Начала» Евклида. Наша школьная геометрия заимствована из нее практически полностью. Строгие, совершенные геометрические методы греков, вдохновенно изученные в дискуссионных кружках и свободных академиях XVII века, привели к рождению в 1665 году нового исчисления — математического анализа. Когда это произошло, свежие математические идеи быстро распространились среди европейских интеллектуалов, и даже «просвещенные деспоты» второй половины xVlll столетия — Фридрих II, Людовики XV и XVI, Екатерина II начали стремиться окружать себя математиками. Новое исчисление наряду с искусством фехтования и менуэтом приобрело социальную значимость и стало классическим, а последующая история убедительно продемонстрировала, насколько важной оказалась диффузия математических идей для развития науки и техники.
Наглядное изображение важных геометрических и топологичесиих объектов — симплексов, особых (нам говорят математини, сингулярных) точек. Симплексы служат простейшими «кирпичами», из которых собираются более сложные геометрические объекты. На этом рисуние симплексы (тетраэдры) образуют сложную «звезду» — объект, который тоже часто встречается в современной геометрии и топологии.
В чем же причина того, что изысканный и получивший общественное одобрение математический анализ, в свою очередь, стимулировал прогресс общества? Прежде всего благодаря механике Ньютона, которую сегодня чаще называют динамикой. Динамика — это область, лежащая между математикой и другими дисциплинами, можно сказать, что это наука-посредник, делающая математику менее эзотерической — доступной лишь избранным «высоколобым». Динамика в отличие от статики изучает не ситуации, а процессы, исследует всевозможные изменения состояний, скорости таких изменений, быстроту изменения этой скорости и так далее. Все это наблюдается в природе (проследите, например, за полетом мухи), и сегодня мы принимаем существование динамических понятий как должное, начисто забыв о том, что сама концепция эволюции какого-либо начального состояния (заданного, как принято было считать, конечно же, господом богом) вошла в человеческое сознание лишь в XIV веке.
Представим себе идеальный детективный роман. В таком романе нам выдаются все необходимые и важные факты, отправляясь от которых мы в принципе можем сразу же раскрыть преступление. Правда, эти факты часто выглядят странными, малозначащими, слабо связанными друг с другом, а то и вообще противоречивыми, и тогда мы вынуждены создавать целый набор собственных версий о том, как будут развиваться события. Но лишь одна из всех версий приводит к разгадке тайны, нащупать эту единственную нить непросто, и зачастую мы предпочитаем даже не делать попыток объяснить все обстоятельства криминальной истории с помощью «чистого» мышления. Страница за страницей плетемся мы на поводу у автора, с нетерпением дожидаясь, когда же наконец он приступит к разоблачениям в конце книги.
Развитие детективного сюжета — пример динамической модели. Действительно, некоторое начальное состояние, исходная ситуация в человеческой группе приобретают еще и временное измерение, с каждой перелистываемой нами страницей начинают «развертываться» вдоль оси времени. Иными словами, на вопрос: что изучает динамика?— можно кратко ответить: поведение.
Законы, управляющие поведением изучаемого объекта (как иногда выражаются физики; оператор эволюции), далеко не всегда известны с достаточной точностью, чтобы можно было предвидеть финал. Более того, даже в тех случаях, когда эволюция описывается сравнительно простыми уравнениями, ее конечный результат может оказаться непредсказуемым. Что же, выходит, делать какие-либо выводы о поведении динамической системы — бесполезное занятие, и в мире царят хаос, случайность, индетерминизм? Несмотря на то, что во многих случаях развитие событий, действительно становится хаотическим, в современной математике недавно появилась методы, позволяющие очень многое узнать о динамической системе как бы а priori, то есть не дожидаясь, пока она пройдет все этапы своей эволюции. Эти методы можно в каком-то смысле уподобить подходу Шерлока Холмса, который всегда заранее знал, как должны развиваться события, а зародились новые идеи примерно в то же время, когда А. Конан Дойл посадил в кресло-качалку своего легендарного сыщика. Но самое интересное состоит в том, что новые, посленьютоновские методы динамики почти целиком сводятся к геометрии.
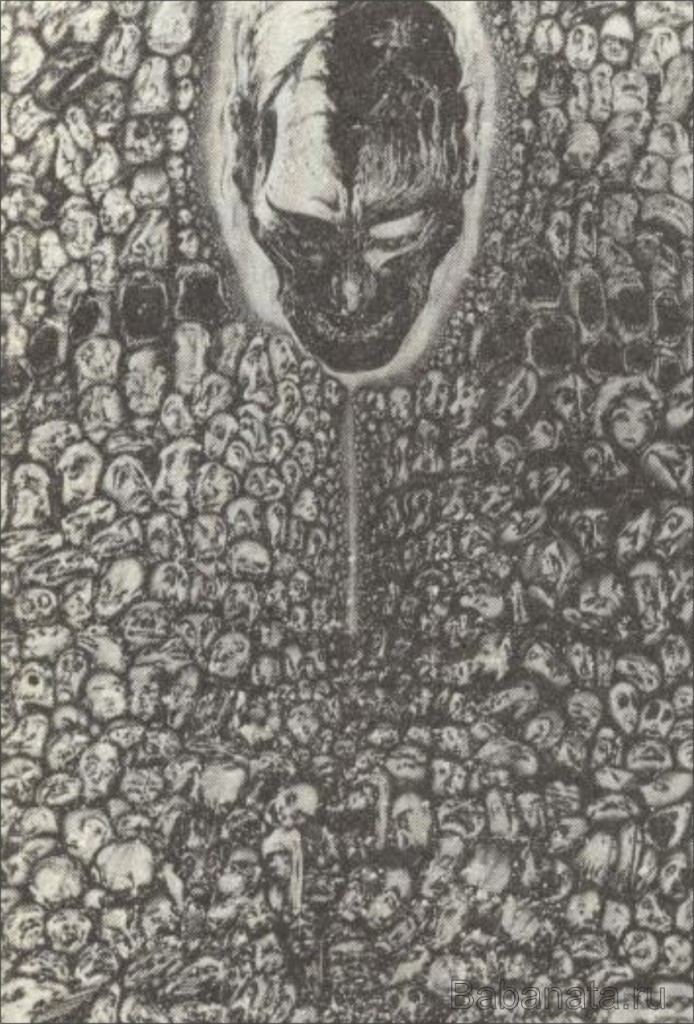
Условное изображение понятий математической бесконечности и топологических преобразований. Бесконечный ряд меняющихся человеческих пиц, предельные точки — такие, в окрестности которых накапливается бесконечно много объектов. В современной геометрии большую роль играет понятие гомеоморфизма, то есть такого топологического преобразования фигур, при котором не меняются их качественные характеристики (например, число дырок в фигуре).
Основы геометрической теории динамических систем были заложены выдающимся французским математиком Анри Пуанкаре. Ключевым понятием этой теории стало представление о фазовом портрете. Первым делом, чтобы нарисовать такой портрет, Пуанкаре ввел набор всех возможных состояний системы — пространство состояний или фазовое пространство. И тогда оказалось, что на языке геометрической модели динамика системы, то есть ее эволюция, определяется ячеистой структурой, состоящей из так называемых бассейнов, которые отделены друг от друга особыми кривыми — сепаратрисами (separer—по-французски разделять). Бассейнами отдельные ячейки назвали потому, что внутри каждой из них находится притягивающее ядро — аттрактор, в который стекаются все фазовые траектории из данного бассейна. Как правило, притяжение динамической системы каким-нибудь ее аттрактором происходит довольно быстро; поэтому те состояния, которые мы в действительности наблюдаем, и есть аттракторы. Фундаментальные понятия современной динамики можно «пощупать» на простом примере шарика, скатывающегося в лунку. Начальное положение шарика быстро забывается, а переходный процесс скатывания длится весьма непродолжительное время, и очень скоро шарик начнет устойчиво кататься в лунке, постепенно из-за трения приближаясь к ее центру. Этому устойчивому положению соответствует одна из разновидностей аттракторов — предельная точка (узел), а та окрестность, из которой шарик обязательно скатится в ямку,—бассейн. Таким образом, портрет динамической системы, на котором изображены бассейны и аттракторы, дает о ней почти исчерпывающую информацию.
Математическая фантазия на темы средневековых мифов и легенд. Из цикла графических работ А. Т. Фоменко «Беседы с авторами XVI —XVII веков».
Обобщая пример со скатывающимся шариком, мы можем научиться моделировать довольно сложные динамические системы. На 6—7 страницах цветной вкладки показаны основные этапы такого геометрического моделирования. Правда, иной раз поведение рассматриваемого объекта оказывается намного сложнее эволюции катающегося в ямке шарика, и для геометрической модели поведения уже будет недостаточно простого координатного (плоского) пространства состояний. Тогда ему на смену приходят более сложные математические объекты, называемые многообразиями. По существу, это понятие обобщает представление о кривой поверхности: многообразия сделаны как бы из кусков плоских поверхностей, которые согнуты и склеены по определенным правилам. Так или иначе, модель поведения начинается с выбора пространства состояний, в котором удается изобразить наблюдения, производимые над объектом. Последним может быть что угодно: лабораторный прибор, ядерный реактор, биологический организм или социальная группа. Затем в пространстве состояний нужно как-то изобразить типичные закономерности перехода объекта от одного состояния к другому, правила, по которым одна ситуация сменяет другую. Как это сделать? Оказывается, рецепт предложил еще Ньютон в 1665 году: нужно всюду задать мгновенные скорости. В самом деле, скатывающийся в лунку шарик в каждой точке своей траектории имеет определенную по величине и направлению скорость, а это означает, что переход шарика в каждую следующую точку определен однозначно. Другими словами, поставив каждой точке многообразия в соответствие свою скорость, то есть задав векторное поле скоростей, мы полностью охарактеризуем нашу динамическую систему. Ее эволюцию можно представить себе как некоторый поток, текущий в фазовом пространстве, его так и называют — фазовый поток.
Если для какого-то объекта или, скажем, организма удалось бы построить такую геометрическую модель, то полностью описать его поведение — уже дело техники (в частности, вычислительной). Математические инструменты почти автоматически нарисуют фазовый портрет, и чем аккуратнее удастся изобразить траектории, тем точнее можно предсказать развитие начальной ситуации в течение некоторого промежутка времени. В прикладных дисциплинах, например, в теории колебаний и радиотехнике, такие предсказания поведения оказываются весьма успешными.
Но это еще не все. Может быть, самое важное из всего, что может предложить динамическая теория, это предсказание весьма отдаленного будущего. Иными словами, геометрическая теория динамических систем способна выдавать вполне содержательные прогнозы того, как станет себя вести изучаемый объект через неопределенное или даже бесконечное время (как говорят, асимптотически). Правда, для большинства динамических систем такие предсказания математиков носят скорее качественный, чем количественный характер, но их ценность от этого ничуть не меньше. Разве не интересно, например, было бы узнать, не упадет ли когда-нибудь Земля на Солнце?
С. ПАНКРАТОВ.
Современная хронология, сложившаяся в результате разработки идей и фундаментальных трудов И. Скалигера (1540-1609) и Д. Петавиуса (1583-1652), рассматривается как область знаний, в целом завершенная и нуждающаяся лишь в отдельных уточнениях, не затрагивающих всего здания хронологии в целом. Тем не менее оказывается, что принятая сегодня хронология древности несет в себе глубокие противоречия.
Уже историки XVIII—XIX веков отмечали многие, мягко говоря, «странности» в трудах историков Древнего Рима. Это и неудивительно. Ведь традиционная версия римской хронологии покоится на весьма шатких основаниях.
Например, между различными датировками такого важного события, как основание Рима, есть расхождение в 500 лет. Такое колебание существенно сказывается на датировке множества документов, ведущих счет лет «от основания Рима» (такова, в частности, «История» Тита Ливия). Согласно традиционной хронологии, падение Трои произошло за 500 лет до основания Рима, но, согласно другой версии, Троянская война разразилась непосредственно перед основанием Рима.
Существенные расхождения между хронологическими данными древних источников и установленной в XVI веке версией хронологии были вскрыты и в других разделах исторической науки.
Сложная ситуация сложилась вокруг такого известного древнего документа, как список царей, якобы составленный шумерскими жрецами. Известный археолог Л. Вулли прямо признавал эту хронологию бессмысленной. Более того, оказалось, что последовательность династий в жреческом списке установлена произвольно. Громадная древность, по сей день приписываемая этим спискам, противоречит археологическим данным. Сообщая о раскопках царских гробниц в Месопотамии, тот же Вулли рассказывает о серии находок золотых туалетных принадлежностей. Лучший эксперт заявил, что это вещи арабской работы XIII века! Впрочем, это не помешало Вулли со снисходительным высокомерием заявить, что эксперт просто не подозревал, «что столь высокое искусство могло существовать в III тысячелетии до нашей эры». Приверженность к традиционной хронологии не позволила ученому даже допустить мысль о том, что, может быть, эксперт все-таки прав в своей датировке.
Значительные трудности сопровождают и попытки правильной географической локализации многих древних событий. Например, Неаполь («новый город») присутствует в древних хрониках в нескольких вариантах: Неаполь в Италии, Карфаген, Неаполь в Палестине, Неаполь скифский. По традиционной хронологии считается, что Троя была разрушена в XII-XIII веках до н. э. Однако в средние века пользовалась известностью итальянская Троя, существующая до наших дней. Этот город упоминается и у многих византийских историков, причем многие из них отождествляют Трою с Иерусалимом. Юг же Италии в средние века назывался Великой Грецией. Сегодня считается, что Вавилон был расположен в современной Месопотамии. Другого мнения придерживались авторы многих древних текстов. Некоторые из них помещают Вавилон в Египет более того, локализуют в Египте смерть Александра Македонского. Они определяют Вавилон как греческое название поселения, расположенного напротив пирамид. Не они ли и породили предания о Вавилонской башне? Вавилоном в средние века называли также Каир, предместьем которого стало это поселение. Достаточно часто средневековые авторы подразумевают под Вавилоном Рим, а визинтийцы чаще всего называют Вавилоном Багдад.
Таким образом, налицо не только существенная неоднозначность в датах, но и в географической локализации древних событий.
Археология также базируется на безраздельном субъективизме и на традиционной версии хронологии. Вновь находимые предметы сравнивают с «похожими» находками, датированными ранее на основе традиции. Здесь абсолютно не ясно, что подразумевается под «похожестью».
Яркий пример проблем, возникающих при датировке археологического материала,— раскопки Помпеи. Автор XV века Дж. Саннацар писал: «Мы подходили к городу (Помпее.-Ред.), и уже виднелись его башни, дома, театры и храмы, не тронутые веками».
Но ведь Помпея считается разрушенной и засыпанной вулканическим пеплом Везувия в 79 году н. э.! Дабы как-то сгладить явно скандальную ситуацию, археологи вынуждены расценивать слова Саннацара так: в XV веке некоторые из зданий Помпеи выступали над слоем пепла… Получается, что потом город был засыпан вторично! И никого не смущает явная нелепость этого заявления.
В XX веке археологи и историки обратили внимание на странный процесс: подавляющее большинство древних памятников за последние двести—триста лет (то есть с того момента, когда за ними стали вестись непрерывные наблюдения) почему-то стали разрушаться сильнее и быстрее, чем за предыдущие якобы столетия и тысячелетия. Стало обычаем ссылаться для объяснения этого процесса на современную промышленность и загрязнение окружающей среды, но никто не исследовал влияния современной цивилизации на каменные строения. Естественно и логично было бы предположить, что все эти постройки не такие древние, как это утверждает традиционная версия хронологии, и разрушаются они естественным порядком и с естественной скоростью.
Все вышесказанное убедительно доказывает, что традиционная хронология исторических событий далека от совершенства, грешит субъективизмом и весьма широкими допущениями. Чтобы преодолеть трудности создания объективной хронологии, надо попытаться взглянуть на предмет под новым углом зрения и создать некую независимую, не базирующуюся на субъективных оценках методику датировки событий. По мнению автора, наиболее пригоден для этой цели подход, основанный на статическом анализе различных числовых характеристик, содержащихся в исторических текстах.
Какие характеристики могут быть подвергнуты математической обработке?
Прежде всего это функция объемов погодных текстов, то есть объемы тех фрагментов исторических текстов, которые описывают события одного года. Далее — частоты употребления полных имен исторических персонажей, упомянутых в исследуемых текстах. Иногда в текстах встречаются приписывание деяний ранних героев более поздним деятелям, литературные штампы, узаконенные повторы. Такие дубликаты можно выявлять и изучать с помощью функций частот параллельных фрагментов текстов. Есть еще одна характеристика — средний возраст имен, упомянутых в каждом фрагменте текста, описывающего события одного года. Ценные результаты можно получить из анализа описаний астрономических событий в древниих текстах — затмений, вспышек звёзд, комет, и т.д.
Далее выяснилось, что имена персонажей, впервые появившиеся в данном поколении, в дальнейшем вытесняются новыми именами, и можно говорить о затухании частот упоминания древних имен. Из анализа затуханий можно делать ценные хронологические выводы. Иногда случается, что после долгого перерыва наступает период возрождения древних имен. Ценные результаты можно получить из анализа амплитуды и частот этих «возрождений».
Таким образом, удалось разработать семь методик, основанных на статистическом анализе упомянутых выше количественных характеристик текстов. Каждая из семи методик строится по одной схеме: сначала формулируется статистическая гипотеза (модель), предназначенная для исследования какого-либо конкретного процесса. Затем модель математически формализуется, вводятся числовые коэффициенты, позволяющие количественно измерять и оценивать отклонения экспериментального поведения или иной количественной характеристики процесса от теоретически предсказанной. Далее модель проверяется на экспериментально достоверном материале. Если модель подтверждается, то методику датирования можно применять для уточнения хронологических данных.
Разработанные методики были экспериментально проверены на материале средневековой истории XIII—XVIII веков. Проверка подтвердила их эффективность.
Вторым этапом было применение методик к материалу древней истории. В результате исследования наряду с подтверждением известных датировок были обнаружены весьма существенные отклонения от них и некоторые статистические закономерности в глобальной хронологии. В сравниваемых текстах обнаружены многочисленные параллели, историографическое родство, зависимость текстов, «возрождение» терминологии и имен и многое другое. В дальнейшем для краткости будем говорить просто об аналогах, понимая под этим весь комплекс перечисленных понятий.
Третьим, заключительным этапом исследований стал анализ глобальной хронологии древней и средневековой истории Европы, Средиземноморья, Египта, Ближнего Востока. Главным результатом этого этапа стало выявление внутренней структуры глобальной хронологической карты — ГХК.
ГХК — это графическое изображение исторической информации, расположенное вдоль горизонтальной’оси времени. Исторические и хронологические данные обширных таблиц Блера и четырнадцати других аналогичных таблиц, дополненные информацией из 228 текстов (хроник, летописей и т. д.), содержали в сумме описание практически всех основных событий в указанных регионах на интервале от 4000 года до н. э. до 1800 года н. э. в традиционных датировках. Вся историческая информация графически изображается на плоскости в виде графа-карты, вытянутой вдоль горизонтальной оси времени. Каждая эпоха со всеми событиями была подробно изображена списками и датами событий в соответствующем месте на оси
времени. Каждое событие изображалось точкой или горизонтальным отрезком на плоскости. ГХК представляет собой максимально полный «учебник» по древней и средневековой истории всех указанных выше регионов.
Сопоставление вычисленных для различных периодов функций выявило наличие аналогов-дубликатов. Попытка систематизировать многочисленные аналоги показала, что они естественно группируются в некие блоки, которые для наглядности были обозначены одинаковыми буквами. Всего оказалось шесть разновидностей блоков — К, Н, П, Р, Т, С. Результат — строка Е на рисунке.
Сложность получившейся картины побудила автора попытаться обнаружить закономерность в распределении аналогов. Оказалось, что из строки Е естественным образом вычленяются четыре практически одинаковых слоя — Ct, С2, С3 и С4, смещенных относительно друг друга по оси времени соответственно на 333, 1053, 1778 лет. ГХК есть результат наложения этих сдвинутых слоев друг на друга.
Практически это означает, что известная нам версия глобальной хронологии ранее XIII века н. э. нуждается в весьма существенных уточнениях. Потребуется передатировка целых крупных блоков событий, относимых ныне к глубокой древности. После такой процедуры известная нам письменная история Европы и Средиземноморья сильно сократится. Большинство событий, относимых сегодня к седой древности, расположится на интервале от X до XVII века н. э. Принятая же ныне версия хронологии Скалигера и Петавиуса согласуется с результатами статистического датирования лишь на интервале от XIII до XX века н. э. На интервале X—XIII веков н. э. уже встречаются дубликаты, «спустившиеся» вниз из интервала XIII—XVII веков н. э. Ранее же X века н. э., вероятно, весь «учебник» состоит из дубликатов, оригиналы которых находятся в интервале X—XVII веков н. э. Это означает, что истинная история, имевшая место до X века н. э., нам неизвестна.
Современные историки ввели в употребление такое понятие, как «средневековый анахронизм». Прошлое в средневековых произведениях литературы и живописи рисуется в тех же категориях, что и современность. Бибпейские и античные персонажи изображаются на картинах в средневековых костюмах; на порталах соборов ветхозаветные цари и патриархи соседствуют с античными мудрецами и евангелическими персонажами; крестоносцы в конце XI века, воюя в Палестине, убеждены, «что карают не потомков палачей Иисуса Христа, но их самих. Таких примеров можно прибести бессчетное множество.
Современные историки, будучи не в состоянии отказаться от привычной, традиционной хронологии, считают, что средневековье в грандиозных масштабах «смешало эпохи и понятия». Но так ли это?
Анатолий Фоменко
Журнал «ЧиП»
